This document will be available to you during tests and exams
- Jupiter Keyboard Shortcut Cheat Sheet
- Jupyter Notebook Cheat Sheet
- Jupyter Notebook Markdown Cheatsheet
7.1. Table of Contents¶
Jupyter-Notebook-Cheatsheet-Keyboard-Shortcuts Download JupyterNotebookCheatSheet Download This is the basics of Jupyter Notebook to get you up and running in using Notebooks to make your programming experience great for more advance stuff stay tuned. This really useful if you need to have a look at what Jupyter logs out since some errors and logs are not visible within the notebooks. For more useful commands and arguments have a look at this Systemd cheatsheet. Now, you should be able to manage and monitor your Jupyter service with Systemd. Jupyter Notebook Markdown Cheatsheet April 9, 2020 SqlBak mike Jupyter Notebook is a great tool for data analysis. And one of its greatest features is that you can easily combine runnable code with rich-text annotations. Important books, cheat sheet, notebooks for machine learning. Boilerplate r books jupyter-notebook ml kaggle cheatsheet kaggle-titanic notebooks Updated Feb 5, 2019.
Holoviews cheatsheet. In 7: import pandas as pd import numpy as np import holoviews as hv from holoviews import opts from holoviews import streams import param hv. Extension ('bokeh', 'matplotlib') # Set dark theme from bokeh.themes import builtinthemes hv. Renderer ('bokeh'). Theme = builtin.
7.2. Numeric¶
7.3. Basic plotting functions¶
7.4. Symbolic manipulation¶
7.4.1. Imports¶
Symbol definitions
Example controller and system
7.4.2. Working with rational functions and polynomials¶

We often want nice rational functions, but sympy doesn’t make expressions rational by default
The cancel function forces this to be a fraction. collect collects terms.
In some cases we can factor equations:
Obtain the numerator and denominator:
If you want them both, you can use
Convert to polynomial in s
Once we have a polynomial, it is easy to obtain coefficients:

Calculate the Routh Array
To get a function which can be used numerically, use lambdify:
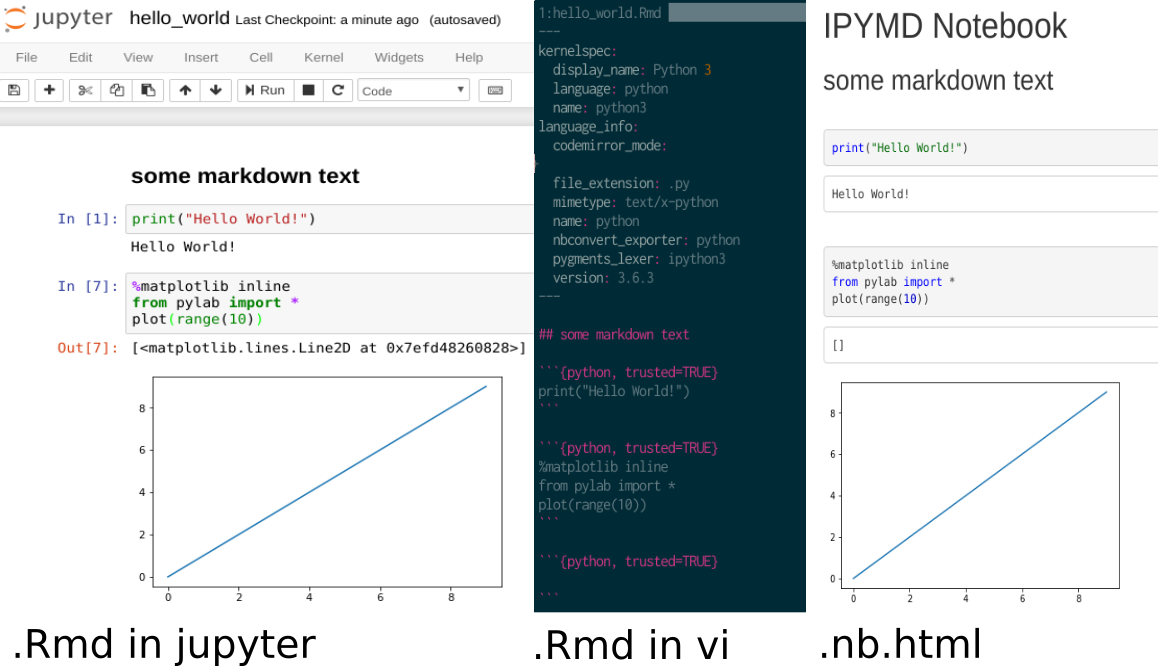
Jupiter Keyboard Shortcut Cheat Sheet
7.4.3. Functions useful for discrete systems¶
Write in terms of positive powers of (z):

Write in terms of negative powers of (z):
Inversion of the (z) transform
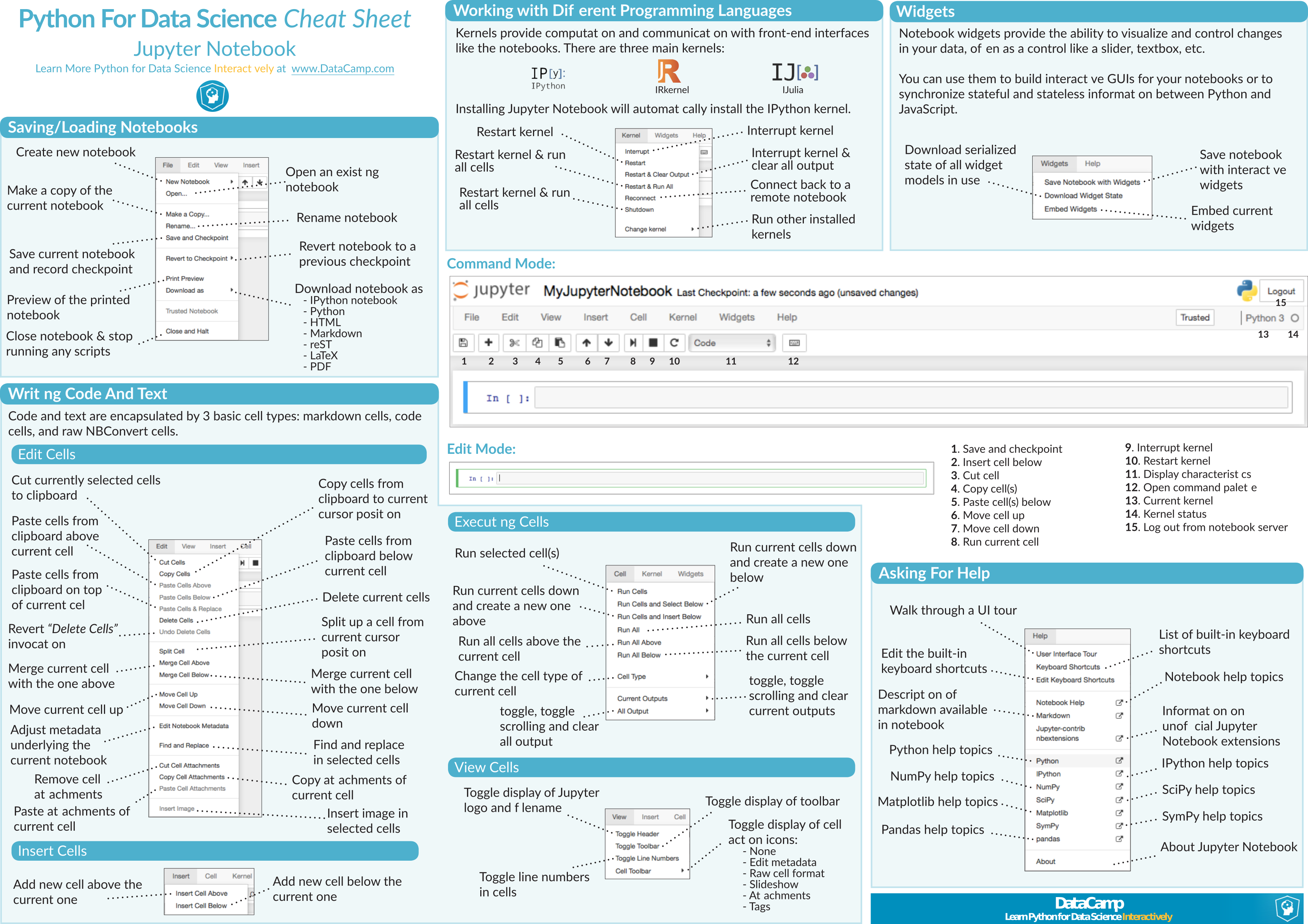
Jupyter Notebook Cheat Sheet
7.5. Equation solving¶
7.5.1. Symbolic¶
7.5.2. Numeric sympy¶
7.5.3. Numeric¶
7.6. Matrix math¶
7.6.1. Symbolic¶
Jupyter Notebook Markdown Cheatsheet
Creation
Determinant, inverse, transpose
Math operations: Multiplication, addition, elementwise multiplication:
7.6.2. Numeric¶
Creation
Determinant, inverse, transpose
Math operations: Multiplication, addition, elementwise multiplication:
